Introduction of fixed-point and floating-point representation

Purpose

The fixed-point and floating-point notations are the basic representations on numerical analysis. In algorithm implementation, the notation frequently switches between fixed-point and floating-point.

For avoiding to forget bit and pieces of representation, I recorded a few pieces of information in this post.

The representation of fixed-point numbers

A flxed-point representation of number consists of three parts: the sign field (1 bit), integer field, and fractional field. For the sign bit, on the computer, 0 is used to represent “+” and 1 is used to represent “-“. (two’s complement)

We can simply represent the format of fixed-point number as SW.F, where S is the sign field, W is the integral length of the parameters, F is the fractional length of the parameters. It is obvious that larger W and F results in a better performance and lower bit error rate, but the hardware design needs a large memory size and sillicon area. Thus, we should do simulation and choose suitable value of SW.F for each parameter in the algorithm.

Example. The 8-bit (S2.5)

\(1 \mid 00 \mid 10000\)

represents \((-0.1)_2 = -0.5\)

The representation of floating-point numbers

A floating-point representation of number is by far more flexible. Any \(x \neq 0\) may be written in the form

\(x = \pm (1.b_1b_2... ) \times 2^n\) (binary version of scientific notation),

called the normalized representation of \(x\). The normalized representation is achieved by choosing the exponent \(n\) so that the binary point “floats” to the position after the first nonzero digit.

Example. The 8-bit

\((-1.101)_2 \times 2^2 = (-110.1)_2 = -6.5\)

Floating‐point to Fixed‐point conversion

In order to implement an algorithm such as communication algorithms and voice recongnition algorithms, etc, the algorithm should be converted floating-point doamin to the fixed-point domain and then it should be described with hardware description language (HDL).

The simple method for floating-point to fixed-point conversion use the following steps:

Step 1. Consider a floating-point variable \(a\)

Step 2. Calculate \(b = a \times 2^F\), where \(F\) is the fractional length of the variable and \(b\) is represented in decimal.

Step 3. Round the value of \(b\) to the nearest integer value

Step 4. Convert \(b\) from decimal to binary representation and name the new variable \(c\)

The new variable c uses \(n\) bits to represent the value of \(b\) in binary.

Example.

Considering a floating-point value is \(a = 3.013\), and fixed-point format is S4.3.

The process of conversoin is

Step 1. \(b = a \times 2^F = 3.013 \times 2^{+3} = 24.104\)

Step 2. \(round(24.104) = 24\)

Step 3. \(c = dec2bin(b) = 11000\)

Step 4. \(c = 00011,000\)

Thus, the corresponding fixed-point value is 00011000. (S4.3)

Conversion of floating-point addition to fixed-point addition

The process of performing this conversion is shown bellowing:

Step 1. Align the binary point of operands by adding zero in the right side of operand, which has smaller fractional

Step 2. Each of operands are converted to fixed-point

Step 3. Perform the addtion with new values

Note. It is necessary to consider one bit for carry since the word length of the addition result is the larger word-length of operands plus one.

Example 1.

Considering two floating-point values a = 3.613 (S3.3) and b = 2.3 (S4.2)

The process to perform this conversion of addition is shown bellowing:

Step 1. \(d = a \times 2^F = 3.613 \times 2^3 = 28.904,\) and \(e = b \times 2^F = 2.3 \times 2^3 = 18.4\)

Step 2. round(28.904) = 29, and round(18.4) = 18

Step 3. add = round(d) + round(e) = 29 + 18 = 47

Step 4. c = dec2bin(add) = 101111

Step 5. c = 00101,111

Thus, the corresponding fixed-point value is 00101111. (S4.3)

Example 2. Norm calculation

Considering a floating-point values a = 3.25 + 4.26 (S3.4)

The process to perform this conversion of norm calculation is shown bellowing:

Step 1. \(d = Re\{b\} \times 2^F = 3.25 \times 2^4 = 52\) and \(e = Im\{b\} \times 2^F = 4.26 \times 2^4\)

Step 2. round(52) = 52, and round(68.18) = 68

Step 3. f = abs(52 + 68i) = 85.6037

Step 4. round(85.6037) = 86

Step 5.dec2bin(86) = 0101,0110

Thus, the corresponding fixed-point value is 01010110. (S3.4)

Note. In the hardware implementation, the CORDIC design is an more efficient fixed-point conversion than above method.

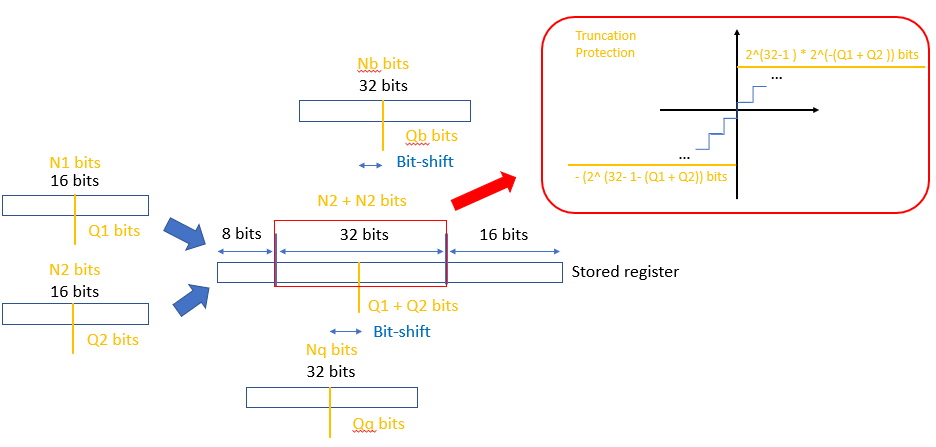
Example 3. Addication using 32-bit register

Considering the addication of two 16-bit registers and storing into 32-bit register. And then add two 32-bit values using 32-bit register. Due to the N-bit number + N-bit number = (N + 1)-bit number, we should use trunction to avoid overflow problem.

The diagrammatic model:

=========== To be continued…. ==========

Reference

[1] Fixed-point and floating-point representations of numbers

[2] Floating‐point to Fixed‐point conversion

[3] The conception of CORDIC

Note

If you have any constructive criticism or advises, leave the comments below or feel free to email me @qazqazqaz850@gmail.com. Hope this post will help! :)