Overview of Basic Graph Traversal Algorithm and Google Testing
01/14/2022 Tags: Algorithms C_C_plus_plus Python[UPDATED: 2022/04/02]
“Graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices (also called nodes or points) which are connected by edges (also called links or lines). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmertically. Graphs are one of the principal objects of study in discrete mathematics.” from Wiki page.
Brief
Recently, I explored the implemenation of graphs, BFS/DFS algorithm and shortest path problem, and discovered its algorithm. It should be grateful that I have learned the fundamentals of mathematics and programming in college, so that I could learn and get a basic understanding of how the graph traversal algorithm work, and further make the computer do it. In this post, I would like to discuss the basic concepts, practice the simple implemenation of BFS and DFS with the directed graph and use googletest to do the unit test.
Graph Search Algorithm
In computer science, a graph is an abstract data type that is meant to implement the undirected fraph and directed graph concept from the field of a graph theory. A graph data structure consists of a finite set of vertices, together with a set of unordered or ordered paired of these vertices. The graph search (also known as graph traversal) algorithm uses a recursion and linked list based stack to determine a route from a single point on a graph to another single point on a graph. In addition to the structure, there are two basic types of graph search: breadth-first search and depth-first search. The major difference between those two type is that the data structure requires a queue (BFS) or stack (DFS).
Directed Graph
Here, I recapped and practiced the simple C++ BFS/DFS implemenation with directed graph initially inspired by Practice Directed Graph then reworked. The basic functions for the directed graph are as follows:
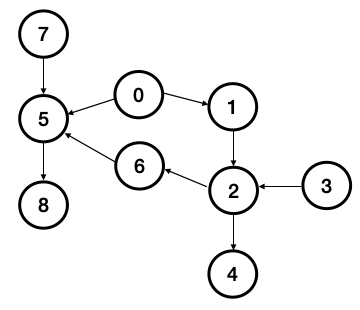 Ordered paired, Unweight and Directed Graph Database
Ordered paired, Unweight and Directed Graph Database- BFS (Breadth-first search): use queue and traverse all the connected nodes
- DFS (Depth-first search): use stack and traverse all the connected nodes
- Detect Cycle in a Directed Graph: check whether the graph contains a cycle or not
- Iterate in a Directed Graph: pointing to all of vertices in the directed graph
Here is the C++ interface of graph traversing:
directedGraph.cc
int main(int argc, char *argv[])
{ // Directed Graph
auto graph_node = new GraphDirected(GraphRepresentation::kRepresentationTypeList);
graph_node->AddEdge(0, 1);
graph_node->AddEdge(0, 5);
graph_node->AddEdge(1, 2);
graph_node->AddEdge(2, 4);
graph_node->AddEdge(2, 6);
graph_node->AddEdge(3, 2);
graph_node->AddEdge(5, 8);
graph_node->AddEdge(6, 5);
graph_node->AddEdge(7, 5);
graph_node->DFS();
graph_node->BFS();
}Here is the Python interface of graph traversing:
directedGraph.py
def main():
dg = DirectedGraph()
dg.add_edge(0, 1)
dg.add_edge(0, 5)
dg.add_edge(1, 2)
dg.add_edge(2, 4)
dg.add_edge(2, 6)
dg.add_edge(3, 2)
dg.add_edge(5, 8)
dg.add_edge(6, 5)
dg.add_edge(7, 5)
p1 = dg1.bfs()
if __name__ == '__main__':
main()Breadth-first Search
Breadth First Search is traversing algorithm where you should start traversing from a selected node (source or parent node) and traverse the graph layerwise thus exploring the neighbour nodes. In other words, it starts at the tree root and explores all nodes at the present depth prior to moving on to the nodes at the next depth level. In addition to the traverse, BFS might be the easiest one to understand because the only data structure it requires is a queue.
Here is the C++ output of BFS traversal route implemenation:
print statement
---------------------
BFS:
0 1 5 2 8 4 6 1 2 3 4 5 6 7 8Here is the python output of BFS traversal route implemenation:
print statement
{1: 0, 5: 0, 2: 1, 8: 5, 4: 2, 6: 2}Depth-first Search
Depth First Search is a recursive algorithm that uses the idea of backtracking. It involves searches of all the nodes by going ahead if possible, else by backtracking. In other words, it starts at the root (selectinh some arbitrary node) and explores as far as possible along each branch before backtracking.
Here is the output of DFS traversal route implemenation:
print statement
---------------------
DFS:
0 5 8 1 2 6 4 1 2 3 4 5 6 7 8Undirected Graph
Here, I recapped and practiced the simple python BFS/DFS implemenation with undirected graph matrix initially inspired by Practice Undirected Graph Matrix then reworked. The basic functions for the undirected graph are as follows:
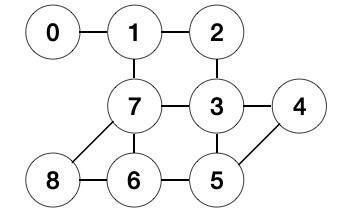
- BFS (Breadth-first search): use queue and traverse all the connected nodes
- DFS (Depth-first search) using recursion: use stack and traverse all the connected nodes using recursion
- DFS (Breadth-first search) using iteration: use stack and traverse all the connected nodes using iteration
undirected_graph_matrix.py
def get_test_graph():
udg = UndirectedGraph(9)
udg.add_edge(0, 1)
udg.add_edge(1, 2)
udg.add_edge(2, 3)
udg.add_edge(1, 7)
udg.add_edge(3, 7)
udg.add_edge(7, 8)
udg.add_edge(3, 4)
udg.add_edge(3, 5)
udg.add_edge(4, 5)
udg.add_edge(5, 6)
udg.add_edge(6, 7)
udg.add_edge(6, 8)
udg.bfs()
udg.dfs_recursive()Here is the output of BFS traversal route implemenation:
print statement
$ python3 undirected_graph_matrix.py
0 1
1 0
1 2
1 7
2 3
7 6
7 8
3 4
3 5Here is the output of DFS traversal route implemenation:
print statement
$ python3 undirected_graph_matrix.py
0 1
1 0
1 2
2 3
3 4
4 5
5 6
6 7
7 8Shortest Path Problem
In graph theory, the shortest path problem is the problem of finding a path betweenn two vertices (or nodes) in a graph such that the sum of the weights of it consitiuent edges is minimized.
The problem of finding the shortest path between two intersections on a road map may be modeled as a special case of the shortest path problem in graphs, where the vertices correspond to intersections and the edges correspond to road segments, each weighted by the length of the segment.
The most important algorithms for solving this problem are:
- Dijkstra’s algorithm: solves the single-source shortest path problem with non-negative edge weight.
- Bellman-Ford algorithm: solves the single-source problem if edge weight may be negative.
Here, I recapped and practiced the Dijkstra’s algorithm with undirected graph initially inspired by Undirected graphs weighted then learned how it implements. The basic functions for the undirected graph are as follows:
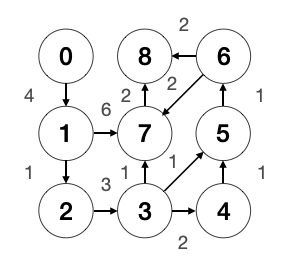
- Add edges in the graph and iterally get vertex: pointing out all of vertices in the undirected graph
- Dijkstra’s algorithm: use priority queue and traversal all the connected nodes
undirected_graph_weighted.py
def main():
g = GraphUndirectedWeighted(9)
g.add_edge(0, 1, 4)
g.add_edge(1, 7, 6)
g.add_edge(1, 2, 1)
g.add_edge(2, 3, 3)
g.add_edge(3, 7, 1)
g.add_edge(3, 4, 2)
g.add_edge(3, 5, 1)
g.add_edge(4, 5, 1)
g.add_edge(5, 6, 1)
g.add_edge(6, 7, 2)
g.add_edge(6, 8, 2)
g.add_edge(7, 8, 2)
shortest_path, distance = g.dijkstra(0, 8)
assert shortest_path == [0, 1, 2, 3, 7, 8] and distance == 11
print("The Shortest path from source 0 to destionation 8 is", distance)
if __name__ == "__main__":
main()Dijkstra’s Algorithm
Dijkstra’a algorithm initially starts with infinite distances and then try to improve them step by step to find the shortest path from a single source to the closest of a set of target nodes on finite graph. Continue this porcess of updating the neighbour intersections with the shortest distance, marking the current intersectiob as visited, and moving onto a closest unvisited intersection until you have marked the destination as visited.
print statement
$ python3 undirected_graph_weighted.py
The Shortest path from source 0 to destionation 8 is 11Exercises
Exercise 1. - Print Binary Tree by BFS (Directed Graph)
The basic functions for this simple exercise is as follows:
- Pass through the binary tree’s object.
- Print out the binary tree by BFS (Breadth-first search) - use queue and traverse all the nodes
printBFS.cc
void PrintBFS(BSTNode * node)
{
std::queue<BSTNode*> node_queue;
BSTNode* current;
node_queue.push(node);
while (! node_queue.empty()) {
current = node_queue.front();
node_queue.pop();
if (current != nullptr) {
std::cout << current->data << " ";
if (current->left != nullptr) node_queue.push(current->left);
if (current->right != nullptr) node_queue.push(current->right);
}
}
}Exercise 2 - Shortest Distance from All Buildings by BFS (Directed Graph)
You want to build a house on an empty land which reaches all buildings in the shortest amount of distance. You can only move up, down, left, and right. You are given a 2D grid of values 0, 1, or 2, where:
- Each 0 marks an empty land which you can pass by freely.
- Each 1 markd a building which you cannot pass through.
- Each 2 marks an obstacle which you cannot pass through.
Example: Input: [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]], Output: 7
Explanation: In this example, there are three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2).

The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal. So return 7.
Solution
shortestDistance.cc
int Solutions::shortestDistance( std::vector< std::vector<int> > & grid )
{
int row = grid.size(), column = grid[0].size();
std::vector< std::vector<int> > distance(row, std::vector<int>(column, 0));
std::vector< std::vector<int> > visit(row, std::vector<int>(column, 0));
int num_building = 0, ans = INT_MAX;
// do BFS
for (int i = 0; i < row; ++i) {
for (int j = 0; j < column; ++j) {
// parent node (building)
if (grid[i].at(j) == 1) {
num_building ++;
auto tmp_grid = grid;
bfs(i, j, tmp_grid, distance, visit);
}
}
}
// find the shortest distance
for (int i = 0; i < row; ++i) {
for (int j = 0; j < column; j++) {
if (visit[i].at(j) == num_building)
ans = std::min(ans, distance[i].at(j));
}
}
return ans == INT_MAX ? -1: ans;
}
void Solutions::bfs(int column, int row, std::vector< std::vector<int> > &grid,
std::vector< std::vector<int> > &distance, std::vector< std::vector<int> > &visit)
{
// assigns starting point into parent node
std::queue< std::pair<int, int> > to_visit; // BFS
to_visit.push( std::pair<int, int>(column, row));
int step = 0;
// traversing from source (parent node)
while (!to_visit.empty()) {
// exploring 2D grid
int curDepth = to_visit.size();
for (int i = 0; i < curDepth; ++i) {
int xx = to_visit.front().first;
int yy = to_visit.front().second;
to_visit.pop();
// meet the boundary
if (xx == grid.size() || xx < 0 || yy == grid[0].size() || yy <0) continue;
// Only empty land which you can pass by freely
if (step != 0 && grid[xx].at(yy) != 0) continue;
// Update Status
visit[xx].at(yy)++; //how many visitor have visited here
distance[xx].at(yy) += step;
grid[xx].at(yy) = -1; // visited
to_visit.push(std::pair<int, int>(xx+1, yy)); // Up
to_visit.push(std::pair<int, int>(xx-1, yy)); // Down
to_visit.push(std::pair<int, int>(xx, yy+1)); // Right
to_visit.push(std::pair<int, int>(xx, yy-1)); // Left
}
step ++;
}
}The solution was initially inspired by Shortest Distance and then reworked. The basic functions for caculating the shortest distanc are as follows:
- Traversing 2D grid by BFS algorithm
- Store visited count and distance between two buildings
Unit Test by Google Testing
shortestDistanceTest.cc
TEST_F(SolutionsTest, ShortestDistanceTest)
{
/* Declare the Unit Test object */
leetcode::Solutions solutions;
std::vector < std::vector<int > > grid = { {1, 0, 2, 0 ,1}, {0, 0, 0, 0, 0}, {0, 0, 1, 0, 0} };
EXPECT_EQ( 7, solutions.shortestDistance(grid));
}Exercise 3. - Critical Connections in a Network by DFS (Undirected Graph)
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
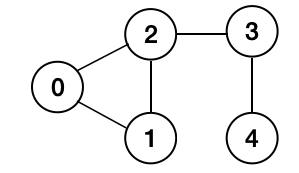
Example: Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3],[3,4]], Output: [[3,4],[1,3]]
Solution
criticalConnections.cc
void undirected_dfs(int curr, int parent, int visited,
std::vector< std::vector<int> > & undirectedgraph,
std::vector<int>& low, std::vector< std::vector<int> > &bridge){
low[curr] = visited ++;
// Exploring the neighbor node
for (auto & nextnode : undirectedgraph[curr]) {
if ( nextnode == parent)
continue;
// unvisited (Depth-first Search)
if (low[nextnode] == 0) undirected_dfs(nextnode, curr, visited, undirectedgraph, low, bridge);
// Assign low value to current node (circle back around to reach)
low[curr] = std::min(low[curr], low[nextnode]);
// Determine the bridge
if (low[nextnode] == visited ) bridge.push_back({curr, nextnode});
}
}
std::vector< std::vector<int> > Solutions::criticalConnections(int n,
std::vector< std::vector<int> > & connections)
{
std::vector< std::vector<int> > undirectedgraph (n);
// constructing undirected graph
for (auto & elem : connections) {
undirectedgraph[elem[0]].push_back(elem[1]);
undirectedgraph[elem[1]].push_back(elem[0]);
}
std::vector< std::vector<int> > bridge;
std::vector<int> low(n);
undirected_dfs(0, -1, 1, undirectedgraph, low, bridge);
return bridge;
}The solution was initially inspired by Leetcode’s Discuss 1: Critical Network and LeetCode’s Discuss, and then reworked. The basic functions for determining critical connections are as follows:
- Constructing undirected graph
- Do a recursive DFS traversal, labeling node with increasing visited time and track the smallest low link value
- Determine critical connection (bridge) according to when the low link value is equal to visited time.
Note that:
- Low link value of a node is defined as the smallest visited time from current node when doing a DFS, including itself.
- Bridge in graphy theory is any edge in a graph whose removal increases the number of connected components.
Unit Test by Google Testing
criticalConnectionsTest.cc
TEST_F(SolutionsTest, criticalConnectionsTest)
{
/* Declare the Unit Test object */
leetcode::Solutions solutions;
std::vector< std::vector<int> > connection = { {0, 1}, {1, 2}, {2, 0}, {1, 3}, {3, 4} };
int n = 5;
std::vector< std::vector<int> > expected_value = { {3, 4} , {1, 3} };
EXPECT_EQ(expected_value, solutions.criticalConnections(n, connection));
}Exercise 4. - Maximum Length of a Concatenated String with Unique Characters by DFS (Undirected Graph)
You are given an array of strings arr. A string s is formed by the concatenation of a subsequence of arr that has unique characters.
Return the maximum possible length of s.
A subsequence is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.
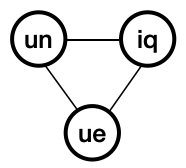
Example 1:
Input: arr = [“un”,”iq”,”ue”] Output: 4 Explanation: All the valid concatenations are:
- ””
- “un”
- “iq”
- “ue”
- “uniq” (“un” + “iq”)
- “ique” (“iq” + “ue”)
Maximum length is 4.
Solution
isUniqieString.cc
int Solutions::maxLength( std::vector< std::string> & arr)
{
int len = 0;
if (arr.size() > 0) return 0;
if (arr.size() == 1) return arr[0].size();
checkLen( arr, "", 0, len)
return len;
}
// undirected DFS ( graph of string )
void Solutions::checkLen( std::vector<std::string> & arr, std::string graphstr, int index, int& count )
{
if (isUniqieString(graphstr)) {
count = graphstr.size() > count ? graphstr.size(): count;
}
// recursive
for (int i = index; i < arr.size(); ++i) {
checkLen(arr, graphstr+arr[i], i+1, count);
}
}
bool Solutions::isUniqieString(std::string s)
{
for (auto & elem : s) {
if (std::count(begin(s), end(s), elem) < 1) return false;
}
return true;
}The basic functions for determining maximum possible length of concatenated string are as follows:
- Concatenated subsequence of string by DFS
- Check the concatenated string is unique characters
- Determine the maximum possible length of concatenated string
Unit Test by Google Testing
maxLengthTest.cc
TEST_F(SolutionsTest, maxLengthTest)
{
/* Declare the Unit Test object */
leetcode::Solutions solutions;
std::vector&;t; std::string> arr {"un", "iq", "ue"};
int expected_value = 4;
EXPECT_EQ(expected_value, solutions.maxLength(arr));
arr = {"abc", "yyy", "def", "csv"};
expected_value = 6;
EXPECT_EQ(expected_value,solutions.maxLength(arr));
arr = {"eva", "jqw", "tyn", "jan"};
expected_value = 9;
EXPECT_EQ(expected_value,solutions.maxLength(arr));
arr = {"photato", "kayak", "banana", "racecar"};
expected_value = 0;
EXPECT_EQ(expected_value,solutions.maxLength(arr));
}Exercise 5. - Surrounded Regions by BFS (Undirected Graph)
Given an m x n matrix board containing ‘X’ and ‘O’, capture all regions that are 4-directionally surrounded by ‘X’.
A region is captured by flipping all ‘O’s into ‘X’s in that surrounded region.
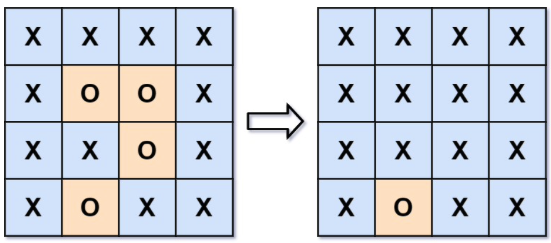
Example: Input: board = [[“X”,”X”,”X”,”X”],[“X”,”O”,”O”,”X”],[“X”,”X”,”O”,”X”],[“X”,”O”,”X”,”X”]] Output: [[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”X”,”X”,”X”],[“X”,”O”,”X”,”X”]]
Solution
surroundedRegions.cc
std::vector< std::vector<char> > Solutions::surroundedRegions( std::vector< std::vector<char> > & board)
{
std::queue< std::pair<int,int> > to_visit;
int row = board.size(), column = board[0].size();
//Getting boundary O's
for(int i=0; i<row ; i++)
{
if(board[i][0]=='O') board[i][0]='U', to_visit.push( {i,0} );
if(board[i][column-1]=='O') board[i][column-1]='U', to_visit.push( {i,column-1} );
}
for(int i=1; i<column-1; i++)
{
if(board[0][i]=='O') board[0][i]='U', to_visit.push( {0,i} );
if(board[row-1][i]=='O') board[row-1][i]='U', to_visit.push( {row-1, i} );
}
// 2-D Grid BFS which's parent node starts from boundary unsorrounded node
while(!to_visit.empty())
{
int curDepth = to_visit.size();
while(curDepth--)
{
int xx=to_visit.front().first, yy=to_visit.front().second;
to_visit.pop();
if(xx+1 < row) if(board[xx+1][yy] == 'O') board[xx+1][yy] = 'U', to_visit.push( {xx+1, yy} ); // RIGHT
if(xx-1 >= 0) if(board[xx-1][yy] == 'O') board[xx-1][yy] = 'U', to_visit.push( {xx-1, yy} ); // LEFT
if(yy+1 < column) if(board[xx][yy+1] == 'O') board[xx][yy+1] = 'U', to_visit.push( {xx, yy+1}); // UP
if(yy-1 >= 0) if(board[xx][yy-1] == 'O') board[xx][yy-1] = 'U', to_visit.push({xx, yy-1}); // DOWN
}
}
//all the unsorrounded O's are re-entered
for(int i=0; i < row; i++)
for(int j=0; j < column; j++)
board[i][j] = board[i][j] == 'U' ? 'O' : 'X';
}The basic functions for determining unsurrounded regions are as follows:
- Get boundary O’s nodes and identify those nodes as unsurrounded node
- Start from unsurrounded node and travers 2D grid by BFS algorithm
- Determine all of unsurrounded nodes and set those as ‘0’
=========== To be continued…. ==========
Reference
[1] Wiki: Graph Theory, Breadth-first search, Depth-first search
[2] Hackerearth: Breadth-first search, Depth First Search
[3] Google testing
[4] Tarjan’s Algorithm: Strongly Connected Components
[5] Wiki: Bridge (graph theory)
[6] Why use Dijkstra’s Algorithm if Breadth First Search (BFS) can do the same thing faster?
Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)
