淺談均攤分析 - Amortized Analysis
01/19/2022 Tags: Algorithms C_C_plus_plus[UPDATED: 2022/07/15]
“In computer science, amortized analysis is a method for analyzing a given algorithm’s complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is, that looking at the worst-case run time can be too pessimistic.” … from Wiki
簡介
最近心血來潮查詢演算法相關的文章,無意間瀏覽到一個技術專有名詞”Amortized Analysis”,中文可以翻作均攤分析或是平攤分析。這專有術語在電腦科學中,用於演算法分析中的方法,常見用於分析資料結構。這篇貼文就淺談相關的知識吧。
均攤分析
為何需要探討Amortized Analysis呢?這方法可藉由分析資料結構各種操作所可能發生的時間,並計算出最壞情況下的操作情況,再加以平均。概念性來說,Amortized Analysis可以分析最壞性能的每次運行的平均時間(runtime),但不能確認實際平均情況的性能。而均攤分析中常見的方式:
- 聚集法(Aggregate method): 分析n次運行的總時間,並決定運行的上限值upper bound T(n),再計算出均攤成本(amortized cost) T(n)/n。
- 記帳法(Accounting method): 類似聚集法,對每個運行分配均攤成本(amortized cost),而前期均攤成本(amortized cost)高於實際成本(actual cost)的運行,可用於累計“credit"供支付後期amortized cost低於actual cost的運行。換句話說,累積的"credit"就等同於連續運行的均攤成本(amortized cost)扣除實際成本(actual cost)。因為"credit"必須維持正數,因此均攤成本(amortized cost)的upper bound必須高於實際成本(actual cost)。一般而言,許多短期運行的累計"credit"是緩慢成長,然而僅罕見長期運行的累計"credit"是劇烈降低。
- 位能法(Potential method): 類似記帳法,藉由"potential"位能函數計算出儲存的"credit",而"amortized cost"可表示為"potential"位能的改變加上"immediate cost“。
CASE STUDY: Incrementing a Binary Counter
一個K位元的二元計數器,從0開往上計算,0, 1, 2, 3 ….。可透過一個K位元的陣列實作,欲求做一連串運算後,這個計算器所做的計算複雜度為多少。

- Traditional worst case analysis: 每變動1位元運行的時間估計上限值upper bound為\(1 + floor(\log(n))\),因此推測總運行的時間為 \(O(n\log(n))\)。
- Aggregate Method: 變動A[0]運行的時間估計為\(n/2^0\), 變動A[1]運行的時間估計為\(floor(n/2^1)\), 變動A[2]運行的時間估計為\(floor(n/2^2)\) ….,依此類推可估算出總運行的時間為\(O(n)\),而均攤成本(amortized cost)為\(O(1)\)。
- Accounting method: 假想成對於低位元從1->0以及0->1的變動收取$2元,其中$1用於支付0->1,剩餘的$1(“credit”)將儲蓄起來供後期使用,至於1->0可藉由前期運行儲蓄的$1來支付。換句話說,維持每位元具有$1的儲蓄”credit”可支付下一次1->0的變動,會計師就用這個位元1的存款付帳而不再花錢。因此,估計總共需要收取$2n元,相當於總運行的時間為\(O(n)\),而均攤成本(amortized cost)為\(O(1)\)。
CASE STUDY: std::vector::push_back(const value_type& __x)
vector 中有兩個的元素:容量 (capacity) 和長度 (size) ,分別代表擁有的空間以及實際儲存了元素的空間大小,概念圖如下:
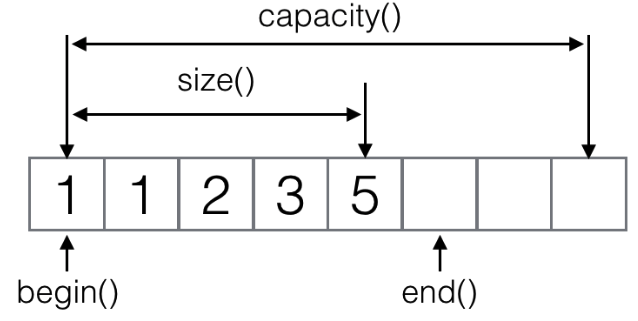
而對於push_back的均攤分析如下:
| Operation | Capacity | Cost |
|---|---|---|
| push_back(1) | 1 | 1 |
| push_back(2) | 2 | 1+1 |
| push_back(3) | 4 | 2+1 |
| push_back(4) | 4 | 1 |
| push_back(5) | 8 | 4+1 |
| ... | ... | ... |
Note: The implementation of std::vector::push_back(const value_type& __x) in STL library
// /usr/local/Cellar/gcc/10.2.0_4/include/c++/10.2.0/bits/stl_vector.h
// [23.2.4.3] modifiers
/**
* @brief Add data to the end of the %vector
* @param __x Data to be added
*
* This is a typical stack operation. The function creates an
* element at the end of the %vector and assigns the given data
* to it. Due to the nature of a %vector this operation can be
* done in constant time if the %vector has preallocated space
* available.
*/
void
push_back(const value_type& __x)
{
if (this->_M_impl._M_finish != this->_M_impl._M_end_of_storage)
{
_GLIBCXX_ASAN_ANNOTATE_GROW(1);
_Alloc_traits::construct(this->_M_impl, this->_M_impl._M_finish,
__x);
++this->_M_impl._M_finish;
_GLIBCXX_ASAN_ANNOTATE_GREW(1);
}
else
_M_realloc_insert(end(), __x);
}總結
均攤分析 - Amortized Analysis 提供一個具有邏輯性思維的分析方式,還可分析許多資料結構,例如:INCREMENT、和MULTIPOP…等。
Reference
- Algorithm - 平攤分析 Amortized Analysis
- Wiki: 平攤分析
- Cornell: Recitation 21: Amortized Analysis Examples
- Amortized Analysis of a Binary Counter
- 超详细STL之基于源码剖析vector实现原理及注意事项
Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)
