Introduction of Asymptotic Complexity
02/04/2022 Tags: Algorithms ProgrammingBrief
When developing in programming, one of critical tasks is that you need to know Big-O, time and space complexity (algorithm complexity). The goal is to estimate the limiting behavior that is used to classify algorithms according to how their run time or space requirements. We might be able to measure how efficient code is based on statement in C++ 11 standard working draft or C++ 14 standard working draft. Here, I would like to sort out several information associated with basic complexity and further practice several simple exercises to estimate those time and space complexity.
The Basic Concept of Asymptotic Complexity
Asymptotic analysis of an algorithm refers to defining the mathematical boundation of its runtime performance. In terms of the most commonly estimated computational resources, it is spoken about the asymptotic time complexity and asymptotic space complexity.
The basic concept to design a good algorithm is that takes less time in execution and saves space during the process. Ideally, we have to find a middle ground between space and time, but we can settle for the average.
Here is the Official Big-O Cheat Sheet Poster:
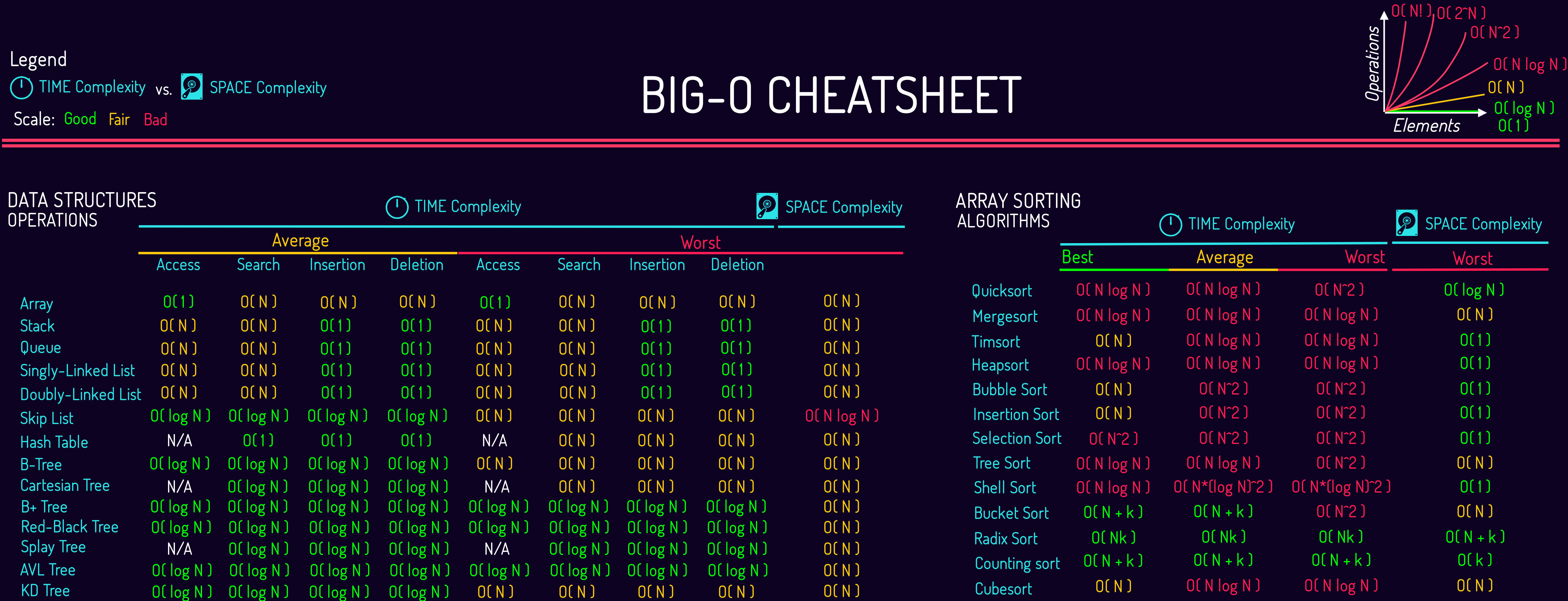
Here is the Common Data Structure Operations:
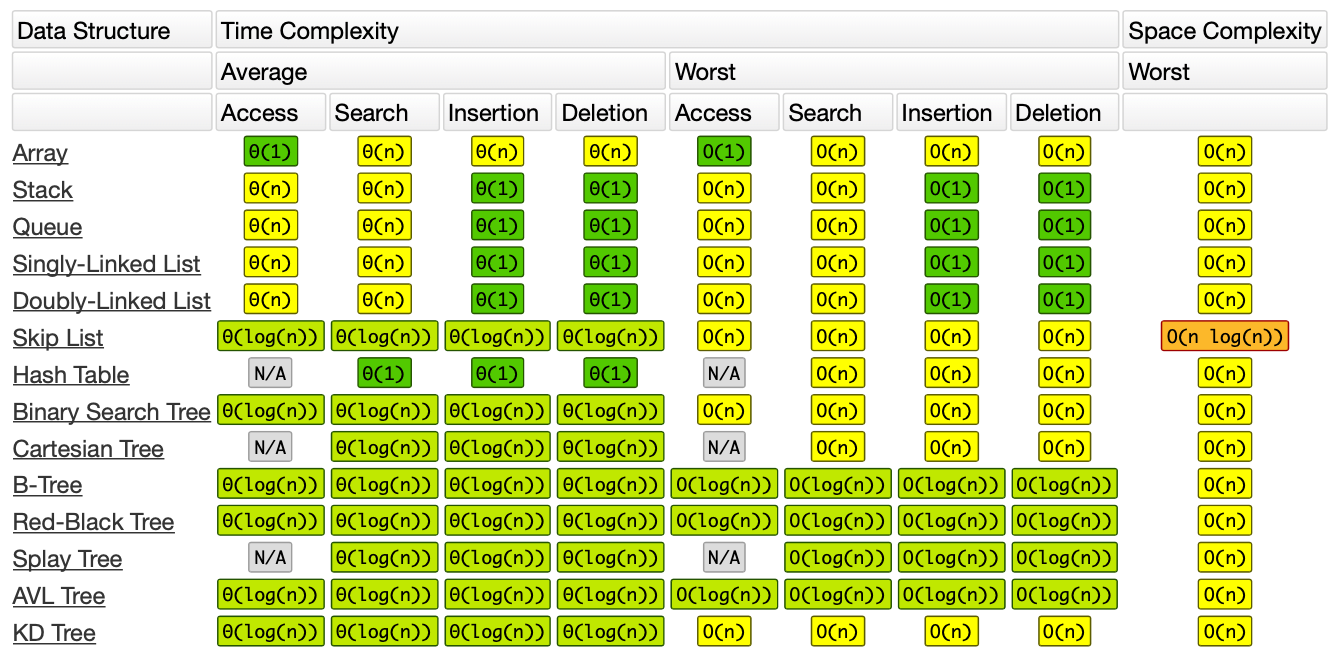
As the above tables, we could know the best, average, and worst case complexities for search, sorting and others algorithms. It might be helpful to save a tone of time.
Note on the several common complexity:
- Complexity of b.count(k): “average case Ο(b.count(k)), worst case Ο(b.size()).”
- Complexity of b.find(k): “average case Ο(1), worst case Ο(b.size()).”
- Complexity of a.erase(q): “average case Ο(1), worst case Ο(a.size()).”
- Complexity of unordered_set: “constant.”
- Complexity of std::sort: “Ο(Nlog(N)) (where N == last - first) comparisons.”
- Complexity of std::reverse: “exactly last - first assignments.”
- Complexity of insert: “average case Ο(1), worst case Ο(a_eq.size()).”
- Complexity of vector: “linear in n.”
- Complexity of vector::push_back: “linear in the number of elements inserted plus the distance to the end of the vector.
Exercise - Min Steps to Make Pilles Equal Height
Alexa is given n piles of equal or unequal heights. In one step, Alexa can remove any number of boxes from the pile which has the maximum height and try to make it equal to the one which is just lower than the maximum height of the stack. Deterßmine the minimum number of steps required to make all of the piles equal in height.
{
int steps = 0;
std::sort(num.begin(), num.end(), std::greater<int> ());
int i = 1;
while ( i < num.capacity()) {
if (num[i] != num[i-1]) {
steps += i;
}
i += 1;
}
return steps;
}Time complexity: O(nlog(n) + n) in the average case.
Space complexity: O(n).
Exercise - Find N Unique Integers Sum up to Zero
Given an integer n, return any array containing n unique integers such that they add up to 0.
{
std::vector<int> v;
for (int i = 1; i<= n/2; ++i) {
v.push_back(i);
v.push_back(-i);
}
if (n%2 != 0) v.push_back(0);
return v;
}Time complexity: O(n) in the average case.
Space complexity: O(n).
Exercise - Minimum Deletions to Make Character Frequencies Unique
A string s is called good if there are no two different characters in s that have the same frequency.
Given a string s, return the minimum number of characters you need to delete to make s good.
The frequency of a character in a string is the number of times it appears in the string. For example, in the string “aab”, the frequency of ‘a’ is 2, while the frequency of ‘b’ is 1.
{
std::vector <int> v(26, 0);
for (auto it : s) v[it - 'a'] ++;
std::map<int, int> mp;
for (int i = 0; i < 26; ++i) mp[v[i]] ++;
int ans = 0;
for (auto it = mp.rbegin(); it!=mp.rend() ; ++it) {
int key = it->first;
int val = it->second;
// not frequencies of elements
if (key == 0 || val == 1) {
continue;
}
// increase the freqnency count after delete characters
int new_val = val - 1;
mp[key -1] += new_val;
ans += new_val;
}
return ansl
}Time complexity: O(n) in the average case.
Space complexity: O(n).
Exercise - Intersection of Two Arrays
Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order.
Approach 1.{
std::unordered_set <int> intersection;
std::sort(nums2.begin(), nums2.end());
for (auto elem : nums1) {
if (binarySearch(nums2, elem)) intersection.insert(elem);
}
return std::vector<int>(intersection.begin(), intersection.end()) ;
}
binarySearch ( std::vector < int > & nums, int target )
{
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left)/2;
if(nums.at(mid) == target) return true;
else if (nums.at(mid) < target) left = mid + 1;
else right = mid;
}
return false;
}Time complexity: O(nlog(n) + m). sort operation is O(nlog(n)) in the average case. for-loop operation is O(m) in the average case.
Space complexity: O(n) in the worst case when all elements in the arrays are different.
Approach 2.{
std::unordered_set<int> set(nums1.begin(), nums1.end()), intersection; // Complexity: Constant.
for (auto elem : nums2) {
if (set.count(elem)) intersection.insert(elem);
}
return std::vector<int>(intersection.begin(), intersection.end());
}Time complexity: O(n) in the average case.
Space complexity: O(m) in the worst case when all elements in the arrays are different.
Reference
[2] Algorithms library: Sorting and related operations
[3] C++ standard working draft N3337 (C++11 + editorial fixes)
[4] C++ standard working draft N4140 (C++14 + editorial fixes)
[5] Complexity:Asymptotic Notation(漸進符號)
Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)
