Louis Better than before

Introduction to the Basic Backtracking Algorithms

03/28/2022 Tags: Algorithms C_C_plus_plus Python

[UPDATED: 2022/06/11]

“Backtracking is a general algorithm for finding solutions to some computational problems, notably constraint satisfaction problems, that incrementally builds candidates to the solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution.” … from Wiki page.

Brief

Backtracking algorithm is one of algorithm paradigms aimed at improving the time complexity of the exhaustive search technique if possible. Backtracking does not generate all possible solutions first and checks later. It tries to generate a solution and as soon as even one constraint fails, the solution is rejected and the next solution is tried. In this post, I would like to discuss the basic concepts, practice how the Backtracking algorithm solves constraint satisfaction problems, such as N-Queens, Verbal Arithmetic Puzzle, and All Paths From Source to Target.

Properties

The basic properties of backtracking algorithm:

  • No repetition and completion: It is a systematic generating method that avoids repetitions and missing any possible right solution. This property makes it ideal for solving combinatorial problems such as combination and permutation which require us to enumerate all possible solutions.
  • Search pruning: Because the final solution is built incrementally, in the process of working with partial solutions, we can evaluate the partial solution and prune branches that would never lead to the acceptable complete solution: either it is invalid configuration, or it is worse than known possible complete solution.

Here, I throw a simple example: Given an integer array nums of unique elements ([1,2,3]), return all possible subsets (the power set).

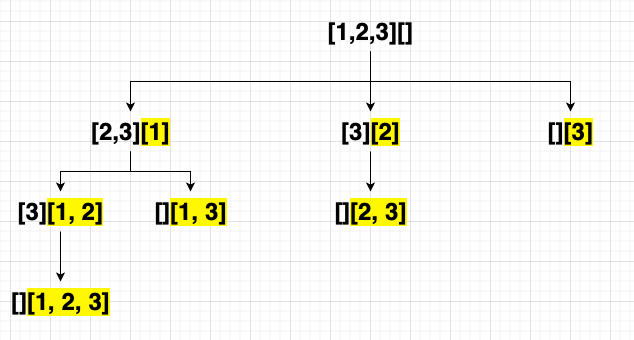
subsets.py 
def subsets(self, nums: List[int]) -> List[List[int]]:
    ans, temp = [], []
    def helper(nums, temp, ans):
        for i in range(len(nums)):
            helper(nums[i+1:], temp + [nums[i]], ans)
        ans.append(temp)
    helper(nums, temp, ans)
    return ans

Here, I throw a simple example: Given an array nums of distinct integers ([1, 2, 3]), return all the possible permutations. You can return the answer in any order.

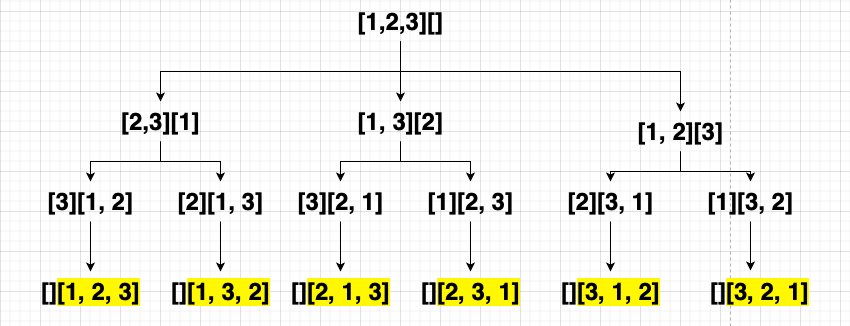
permute.py 
def permute(self, nums: List[int]) -> List[List[int]]:
        ans = []
        def helper(nums, temp, ans):
            if len(nums) == 0:
                ans.append(temp)
                return
            for i in range(len(nums)):
                helper(nums[:i]+nums[i+1:], temp+[nums[i]], ans)
        helper(nums, [], ans)
        return ans

Exercises

  1. Exercise 1 - N-Queens
  2. Exercise 2 - Verbal Arithmetic Puzzle

Exercise 1 - N-Queens

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens’ placement, where ‘Q’ and ‘.’ both indicate a queen and an empty space, respectively.

Example: Input: n = 4, Output: [[“.Q..”,”…Q”,”Q…”,”..Q.”],[”..Q.”,”Q…”,”…Q”,”.Q..”]]

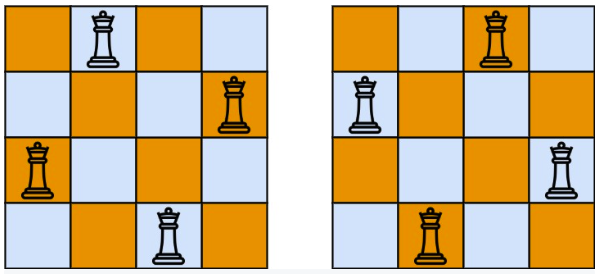
Solution

solveNQueens.cc 
bool is_safe( std::vector< std::string> & board, int row, int col)
{
    // check column
    for (int i = row; i >= 0; --i) if(board[i][col] == 'Q') return false;
    // check left diagonal
    for (int i = row, j = col; i >= 0 && j >= 0; --i, --j)
        if(board[i][j] == 'Q') return false;
    // check right diagonal
    for (int i = row, j = col;  i >= 0 && j < board.size(); --i, ++j)
        if(board[i][j] == 'Q') return false;
    return true;
}
void backtracking_dfs( std::vector< std::string> & board, int row, std::vector< std::vector< std::string> > & result)
{
    if ( row == board.size()) {
        result.push_back(board);
        return;
    }
    for (int i = 0; i < board.size(); ++i) {
        if(is_safe(board, row, i)) {
            // make decision
            board[row][i] = 'Q';
            backtracking_dfs(board, row + 1, result);
            // backtrack to move our queen to next col within same row to get other combinations.
            board[row][i] = '.';
        }
    } 
}
std::vector< std::vector< std::string> > Solutions::solveNQueens(int n) {
    if ( n <= 0 ) return ;
    std::vector< std::vector< std::string> > result;
    std::vector< std::string> board(n, std::string(n, '.'));
    backtracking_dfs(board, 0, result);
    return result;
}

The solution was inspired by LeetCode Discuss and then modified. The basic functions for caculating the all distinct solutions are as follows:

  • Iterate in all the columns to look for safe cells where we can place our queen.
  • If a particular board position is safe as returned by the is_safe function, then placing our queen in that cell and again look for placing our queen in next row.
  • After getting all possible combination from that particular column position of queen in that row, then backtrack to move our queen to next column within same row to get other combinations.

Exercise 2 - Verbal Arithmetic Puzzle

Given an equation, represented by words on the left side and the result on the right side.

You need to check if the equation is solvable under the following rules:

Each character is decoded as one digit (0 - 9). Every pair of different characters must map to different digits. Each words[i] and result are decoded as one number without leading zeros. Sum of numbers on the left side (words) will equal to the number on the right side (result). Return true if the equation is solvable, otherwise return false.

Example: Input: words = [“SEND”,”MORE”], result = “MONEY”, Output: true

Solution

isSolvable.cc 
bool backtracking_verbal( std::vector< std::string> & words, std::string & result, std::vector<int> & chtonum, std::vector<int> & numtoch, std::vector<bool> & nonZeroChars, int index, int pos, int sum)
{
    // reach the end of result
    if (pos == result.size()) return sum == 0;
    // traverse the position and keeping adding words
    if (index < words.size()) {
        // there is no applicable positions for words[index], skip and add next word
        if (pos  >= words[index].size())
            return backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, index + 1, pos, sum);
        char ch = words[index][pos];
        int chindex = ch - 'A';
        // Already selected
        if (chtonum[chindex] != -1) {
            return backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, index + 1, pos, sum + chtonum[chindex]);
        }
        // try to decode each character
        for (int i = 0; i < numtoch.size(); ++i) {
            if (numtoch[i] != 0) continue; // number is used
            if (i == 0 && nonZeroChars[chindex]) continue; // can't use position 0 for non zero chars
            numtoch[i] = chindex;
            chtonum[chindex] = i;
            bool found = backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, index + 1, pos, sum + chtonum[chindex]);
            // backtrack
            numtoch[i] = 0;
            chtonum[chindex] = -1;
            if (found) return found;
        }
        return false;
    } else { // verify whether or not result[pos] and sum % 10 are mapping each other
        int reindex = result[pos] - 'A';
        if (chtonum[reindex] == -1 && numtoch[sum%10] == 0) {
            if (sum % 10 == 0 && nonZeroChars[reindex]) return false;
            chtonum[reindex] = sum % 10;
            numtoch[sum%10] = result[pos];
            bool found = backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, 0, pos + 1, sum / 10);
            if (found) return found;
            chtonum[reindex] = -1;
            numtoch[sum%10] = 0;
            return false;
        } else if (chtonum[reindex] == sum % 10) {
            return backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, 0, pos + 1, sum / 10);
        } else {
            return false;
        }
    }
}
bool Solutions::isSolvable( std::vector< std::string> & words, std::string result) {
    std::vector<bool> nonZeroChars(26, false);
    std::vector<int> chtonum(26, -1);
    std::vector<int> numtoch(10);
    for (auto &word : words) {
        if(word.size() > result.size()) return false;
        if(word.size() > 1) nonZeroChars[word[0] - 'A'] = true;
        std::reverse(word.begin(), word.end());
    }
    if (result.size() > 1) nonZeroChars[result[0] - 'A'] = true;
    std::reverse(result.begin(), result.end());
    return backtracking_verbal(words, result, chtonum, numtoch, nonZeroChars, 0, 0, 0);
}

The solution was copied from LeetCode Discuss and then learn how to implement the solution. The basic functions for caculating whether or not the equation is solvable are as follows:

  • Traverse the position for words[index], try to decode each character and keep adding words
  • If there is no applicable positions for words[index], skip and add next word
  • After getting all possible combination from that particular decoding, then backtrack to try to next decoding.
  • Verify whether or not result[pos] and sum % 10 are mapping each other

=========== To be continued…. ==========

Reference

Related Posts

LIKE THIS ARTICLE? SUPPORT THE AUTHOR WITH OR BUY AUTHOR A COFFEE