Introduction to Bitpartite Graph

“In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.” … from Wiki page.

Brief

A bipartite graph, which is a graph in which the vertices can be put into two separate groups so that only edges are between those two groups, and there are no edges between vertices within the same group. When modeling relations between two different classes of objects, bipartite graph very often arise naturally, such as a graph of football players and clubs or social networking (matching).

Properties

The basic properties of bipartite graph:

• Doesn’t contain an odd cycle (cycle in a graph is a non-empty trail in which only the first and last vertices are equal)
• It is a 2-colorable graph ( graph coloring is a special case of graph labeling).

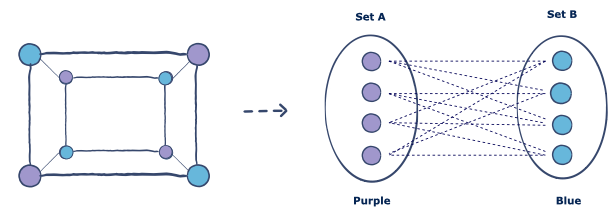
Here, I practiced a simple python isBiparitie implementations with undirected graph matrix. The basic functions for determining whether or not a graph is bipartite are as follows:

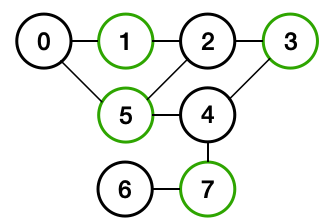
• Push the first node in queue and color the first node
• BFS Traverse the adjacent node and color it
• Determine whether or not the graph is bipartite

def is_bipartite(self):
colorings = {}
to_visit = queue.Queue()
to_visit.put(0)
colorings[0] = 0

while not to_visit.empty():
    node = to_visit.get()
    for next_node in self.get_neighbor(node):
        if next_node not in colorings:
            colorings[next_node] = 1 - colorings[node]
            to_visit.put(next_node)
        elif colorings[nesxt_node] == colorings[node]:
            return False
return True

Exercise

1. Exercise 1 - Is Graph Bipartite?
2. Exercise 2 - Maximum Number of Accepted Invitations

Exercise 1 - Is Graph Bipartite?

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

There are no self-edges (graph[u] does not contain u). There are no parallel edges (graph[u] does not contain duplicate values). If v is in graph[u], then u is in graph[v] (the graph is undirected). The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them. A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

Example: Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]], Output: false

Solution

bool colorable_node(int i, std::vector<int> &color, 
                std::vector< std::vector<int> > & graph)
{
    std::queue<int> q;
    q.push(i);
    color[i] = 0; // color the first node
    while (!q.empty()) {
        int vertex = q.front();
        q.pop();
        for (auto &node : graph[vertex]) {
            if (color[node] == -1) {
                color[node] = 1 - color[vertex];
                q.push(node);
            } else if (color[node] == color[vertex])
                return false;
        }
    }
    return true;
}
bool Solutions::isBipartite( std::vector< std::vector<int> > & graph ) 
{
    int depth = graph.size();
    std::vector<int> color(depth, -1); // all the node are uncolored
    for (int i = 0; i < depth; ++i) {
        if (color[i] == -1) {
            if (!colorable_node(i, color, graph))
                return false;
        }
    }
    return true;
}

The solution was inspired by LeetCode Discuss. The basic functions are same as above description implemented by python.

Exercise 2 - Maximum Number of Accepted Invitations

There are m boys and n girls in a class attending an upcoming party. You are given an m x n integer matrix grid, where grid[i][j] equals 0 or 1. If grid[i][j] == 1, then that means the ith boy can invite the jth girl to the party. A boy can invite at most one girl, and a girl can accept at most one invitation from a boy. Return the maximum possible number of accepted invitations.

Example: Input: grid = [[1,0,1,0],[1,0,0,0],[0,0,1,0],[1,1,1,0]], Output: 3

Solution

bool bitpartiteMatch_dfs(const std::vector&;t; std::vector&;t;int>> & grid, 
                int u, std::vector&;t;bool> visted, std::vector&;t;int> & grils) 
{
    int n = grid[u].size();
    for (int v = 0; v &;t; n; ++v) {
        if (grid[u][v] && !visted[v]) {
            visted[v] = true;
            if (grils[v] &;t; 0 || bitpartiteMatch_dfs(grid, grils[v], visted, grils)) {
                grils[v] = u; // matching
                return true;
            }
        }
    }
    return false;
}
int Solutions::maximumInvitations( std::vector&;t; std::vector&;t;int> > & grid) 
{
    int m = grid.size();
    int n = grid[0].size();
    std::vector&;t;int> grils(n, -1); // unmatched (uncolored)
    int matches = 0;
    // matching process
    for (int i = 0; i &;t; m; ++i) {
        std::vector&;t;bool> visted(n, false);
        if( bitpartiteMatch_dfs(grid, i, visted, grils))
            matches ++;
    }
    return matches;
}

The solution was inspired by LeetCode Discuss. The basic functions for caculating the all distinct solutions are as follows:

• Iterate boys in a class to visit all of unmatched grils
• DFS traversal and invite the adjacent girls in a class
• If grid[i][j] == 1, then ith boy can invite the jth girl to the party
• Recursively trying all possible pairs as we have to get maximum in result

Table of Content

=========== To be continued…. ==========

Reference

• Wiki: Bipartite Graph

• What is a bipartite graph?

Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)