Topological Sorting
04/09/2022 Tags: Algorithms C_C_plus_plus“In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a directed graph traversal in which each node is visited only after all its dependencies are visited.” .. from Wiki page
Brief
A topological sort is a linear ordering of vertices in a directed acyclic graph (DAG). Directed graph can be used to indicate precedence among a set of events. In many applications, we use directed acyclic graphs to indicate precedence among events. For example, in a scheduling problem, there is a set of tasks and a set of constraints specifying the order of these tasks. In this post, I would like to briefly discuss about several practices for the applications of topolgical sort (Course Schedule, Parallel Courses).
Properties
The basic properties of topolgical sorting:
- Every vertex v in the respective ordering occurs before any other vertex to which has edges.
- Topological sorting is not unique.
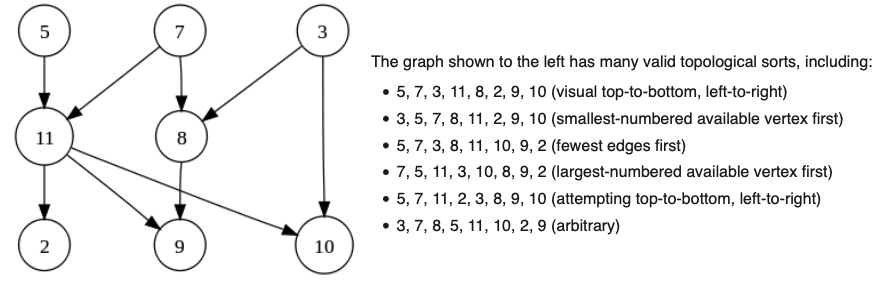
Note: These are three common algorithms for topological sorting
- Kahn’s algorithm: First, find a list of “start node” which have no incoming edges and insert them into a set S; at least one such node must exist in a non-empty actclic graph
- Depth-first search: Loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort or the node has no outgoing edges
- Parallel algorithms: Repeatedly removes the vertices of indegree 0 and adds them to the topological sorting in the order in which they were removed. Since the outgoing edges of the removed vertices vertices are also removed, there will be a new set of vertices of indegree 0, where the procedure is repeated until no vertices are left. Each iteration can be parallelized
Exercises
Exercise 1 - Course Schedule
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1. Return true if you can finish all courses. Otherwise, return false.
Example: Input: numCourses = 2, prerequisites = [[1,0]], Output: true
Solution
coursesSchedule.cc
bool Solutions::canFinish(int numCourse, std::vector< std::vector< int> > & prerequisities) {
std::vector< std::vector<int> > adjacent(numCourse);
// initial all vertices with indegree 0
std::vector<int> indegree(numCourse, 0);
// Creating graph and updates the indegree of the local vertex
for (auto &elem : prerequisities) {
adjacent[elem[0]].push_back(elem[1]);
indegree[elem[1]]++;
}
std::queue<int> q;
// Parallel topological sorting
// iterate through all the courses if indegree is zero then add it to queue
for (int i = 0; i < numCourse; ++i) {
if(indegree[i] == 0) q.push(i);
}
while (!q.empty()) {
int node = q.front();
q.pop();
for (auto &next_node : adjacent[node]) {
indegree[next_node] --;
if(indegree[next_node] == 0) q.push(next_node);
}
numCourse --; // finish the course
}
return numCourse == 0;
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the all distinct solutions are as follows:
- Initialize all vertices with indegree 0
- Create directed graph and update the indegree
- Parallel topological sorting and iterate through all the courses if indegree is zero then add it to queue
- Count how many course will be finished and further determine whether or not all courses can be finished
Exercise 2 - Parallel Courses
There are N courses, labelled from 1 to N.
We are given relations[i] = [X, Y], representing a prerequisite relationship between course X and course Y: course X has to be studied before course Y.
In one semester you can study any number of courses as long as you have studied all the prerequisites for the course you are studying.
Return the minimum number of semesters needed to study all courses. If there is no way to study all the courses, return -1.
Example: Input: N = 3, relations = [[1,3],[2,3]], Output: 2
Solution
parallelCourses.cc
int Solutions::minimumSemesters(int numCourse, std::vector< std::vector<int> > & relations) {
std::vector< std::vector<int> > adjacent(numCourse);
// initial all vertices with indegree 0
std::vector<int> indegree(numCourse, 0);
// Creating graph and updates the indegree of the local vertex
for (auto &course : relations) {
adjacent[course[0] - 1].push_back(course[1] - 1);
indegree[course[1] - 1]++; // study firstly
}
std::queue<int> q;
int semester = 0, count = 0;
// Parallel topological sorting
// iterate through all the courses if indegree is zero then add it to queue
for (int i = 0; i < numCourse; ++i) {
if(indegree[i] == 0) q.push(i);
}
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; ++i) {
int node = q.front();
q.pop();
count ++;
for (auto &next_node : adjacent[node]) {
indegree[next_node] --;
if(indegree[next_node] == 0) q.push(next_node);
}
}
semester ++;
}
return count == numCourse ? semester : -1;
}The basic functions for caculating the all distinct solutions are as follows:
- Initialize all vertices with indegree 0
- Create directed graph and update the indegree
- Parallel topological sorting and iterate through all the courses if indegree is zero then add it to queue
- Count how many courses will be finished and determine the minimum number of semesters needed to study all courses
=========== To be continued…. ==========
Reference
Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)
