Strongly Connected Components
04/12/2022 Tags: Algorithms C_C_plus_plus[UPDATED: 2022/04/26]
“In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time.” … from Wiki.
Brief
A strongly connected component is the portion of a directed graph. The algorithm finds maximal sets of connected nodes in a directed graph. A set is considered a strongly connected component if there is a directed path between each pair of nodes within the set. The use of strongly connected components could find groups of people who are more closely related in a huge set of data.
In this post, I would like to briefly discuss about several the applications of topolgical sort, such as Disconnect Island, Number of Provinces.
Properties
The basic properties of strongly connected components:
- A pair of vertices u and v are said to be strongly connected to each other if there is a path in each direction between them.
- A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph
Note: The usual algorithms for strongly connected components
- DFS-based linear-time algorithms (Kosaraju’s algorithm)
- Reachability-based algorithms
- Generating random strongly connected graphs
Exercises
Exercise 1 - Minimum Number of Days to Disconnect Island
You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1’s.
The grid is said to be connected if we have exactly one island, otherwise is said disconnected.
In one day, we are allowed to change any single land cell (1) into a water cell (0).
Return the minimum number of days to disconnect the grid.
Example: Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]], Output: 2
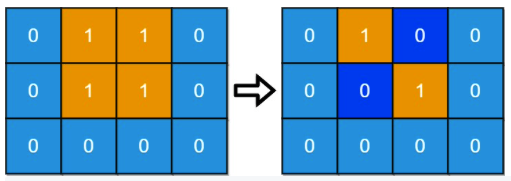
Solution
minDays.cc
void connected_bfs(std::vector< std::vector<int> > & grid, std::vector< std::vector<int> > & visited, int i, int j) {
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
std::queue< std::pair<int, int> > q;
q.push({i, j});
visited[i][j] = 1;
while (!q.empty()) {
auto p = q.front();
q.pop();
int x = p.first, y = p.second;
for (int k = 0; k < 4; k++) {
int xx = x + dx[k], yy = y + dy[k];
// only go through land cell (1)
if ( xx >=0 && xx < grid.size() && yy >= 0 && yy < grid[0].size() && !visited[xx][yy] && grid[xx][yy] == 1) {
visited[xx][yy] = 1;
q.push({xx, yy});
}
}
}
return;
}
int connectedComponents_helper( std::vector< std::vector<int> > & grid) {
int count = 0;
int row = grid.size(), col = grid[0].size();
std::vector< std::vector<int> > visited(row, std::vector<int> (col, 0));
if (row == 0) return 0;
// count connected land
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
if (grid[i][j] == 1 && !visited[i][j]) {
count ++;
connected_bfs(grid, visited, i, j);
}
}
}
return count;
}
int Solutions::minDays( std::vector< std::vector<int> > & grid) {
int connectLand = connectedComponents_helper(grid);
if (connectLand != 1) return 0;
int row = grid.size();
int col = grid[0].size();
// number of days to disconnect the grid
for (int x = 0; x < row; x++) {
for (int y = 0; y < col; y++) {
if (grid[x][y] == 1) {
grid[x][y] = 0;
connectLand = connectedComponents_helper(grid);
if (connectLand != 1) return 1;
grid[x][y] = 1; // backtracking
}
}
}
return 2; // An island is a maximal 4-directionally (horizontal or vertical) connected group of 1's.
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the the minimum number of days to disconnect the grid:
- 2-D BFS-based linear-time traverse to count how many connected land in the grid and further return 0 day if there are more than 2 connected land
- Partition into subgraphs that are changing any single land cell and futher check how many connected connectivity is
- Since an island is a maximal 4-directionally (horizontal or vertical) connected group of 1’s, there can never exist more than 2 days to disconnect island from
Exercise 2 - Number of Provinces
There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.
A province is a group of directly or indirectly connected cities and no other cities outside of the group.
You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.
Return the total number of provinces.
Example: Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]], Output: 2
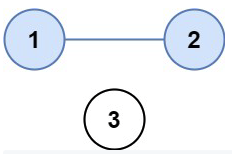
Solution
findCircleNum.cc
void lineartime_dfs(std::vector< std::vector<int> > & isConnected, int index, std::vector<bool> & visted) {
visted[index] = true;
// traverse neighbor city
for (int vertex = 0; vertex < isConnected[index].size(); ++vertex) {
if (!visted[vertex] && isConnected[index][vertex] == 1) {
lineartime_dfs(isConnected, vertex, visted);
}
}
}
int Solutions::findCircleNum(std::vector< std::vector<int> > & isConnected ){
int citys = isConnected.size();
std::vector<bool> visted(citys, false);
int count = 0;
for (int i = 0; i < citys; ++i) {
if (visted[i] == false) {
count += 1;
lineartime_dfs(isConnected, i, visted);
}
}
return count;
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the all distinct solutions are as follows:
- Initialize all cities without visiting
- DFS-based linear-time traverse neighbor city
- Count how many set is considered a connected city
=========== To be continued…. ==========
Reference
Thanks for reading! Feel free to leave the comments below or email to me. Any pieces of advice or discussions are always welcome. :)
