Introduction to Dynamic Programming
05/12/2022 Tags: C_C_plus_plus Programming Python[UPDATED: 2022/06/27]
“Dynamic Programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applicationns in numerous fields, from aerospace engineering to economics.” … from Wiki.
Brief
The dynamic programming (DP) refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner and is just an optimization technique. While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively. Likewise, in computer science, if a problem can be solved optimally by breaking it into sub-problems and then recursively finding the optimal solutions to the sub-problems, then it is said to have optimal substructure.
In other words, the dynamic programming approach describes the optimal plan by finding a rule that tells what the controls should be, given any possible value of the state. For example, if consumption (c) depends only on wealth (W), we would seek a rule c(W) that gives consumption as a function of wealth. Such a rule, determining the controls as a function of the states, is called a policy function. Finally, by definition, the optimal decision rule is the one that achieves the best possible value of the objective. The best possible value of the objective, written as a function of the state, is called the value function.
In this post, I would like to briefly discuss about the properties of dynamic programming and practice several exercises, such as min cost climbing stairs, schedule parallel courses and choose the best time to buy, sell stock and coin Change.
Properties
There are two key properties that a problem must have in order of dynamic programming to be applicable:
- Optimal substructure: the solution to given optimization problem can be obtained by the combination of optimal solutions to its sub-problems. Sub optimal substructures are usually described by means of recursion.
- Overlapping sub-problem: the space of sub-problems must be small, that is, any recursive algorithm solving the problem should solve the same sub-problems over and over, rather than generating new sub-problems.
Simple Example - Fibonacci numbers
Fibobacci numbers are a sequence of numbers where every number is the sum of the preceding two numbers. It starts from 0 and 1 as the first two numbers. This question can be reduced to subproblems of size n - 1 and n - 2. Then, the overlapping subproblem can construct the optimal solution.
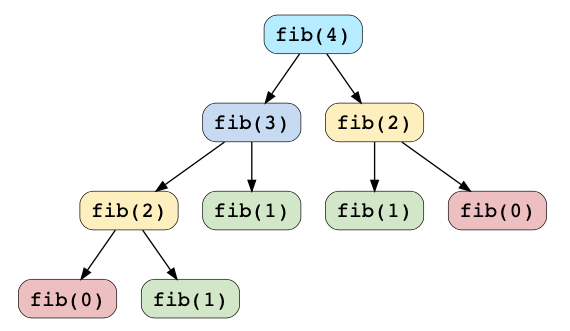
fibonacci.py
@lru_cache(maxsize=None)
def fib(n):
if n < 2:
return n
return fib(n-1) + fib(n-2)Exercises
Exercise 1 - Min Cost Climbing Stairs
You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
Example: Input: cost = [10,15,20], Output: 15
Solution
minCostClimbingStairs.cc
int Solutions::minCostClimbingStairs( std::vector<int> & cost) {
int n = cost.size();
std::vector<int> dp = cost;
for (int i = 2; i < n; i++) {
dp[i] += std::min(dp[i-2], dp[i-1]);
}
return std::min(dp[n-2], dp[n-1]);
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the minimal cost to reach the top of the floor are:
- Iterate over 1 step or 2 step in the stairs and climb the minimal cost.
- Determine the minimal cost when reaching the top of the floor.
Exercise 2 - Best Time to Buy and Sell Stock
You are given an integer array prices where prices[i] is the price of a given stock on the ith day.
On each day, you may decide to buy and/or sell the stock. You can only hold at most one share of the stock at any time. However, you can buy it then immediately sell it on the same day.
Find and return the maximum profit you can achieve.
Example: Input: prices = [7,1,5,3,6,4], Output: 7
Solution
maxProfit.cc
int Solutions::maxProfit( std::vector<int> & prices) {
int curHold = INT_MIN, curProfit = 0;
for (const int stockprice: prices) {
int prevHold = curHold, preProfit = curProfit;
// either keep holding stock in hand, or buy in new stock today at stock price
curHold = std::max(prevHold, preProfit - stockprice);
// either keep having no stock in hand, or sell out the stock today at stock price
curProfit = std::max(preProfit, prevHold + stockprice);
}
// Max profit must come from notHold
return curProfit;
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the maximum profit are the same.
- Keep mointor how much stock in hand and net profit every day
- Return the max profit
Exercise 3 - Parallel Courses II
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.
In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.
Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.
Example: Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2, Output: 3
Solution
minNumberOfSemesters.cc
int find_min_semester( std::vector< std::vector<int> > relations, std::vector<int> & bitmask, int mask, int k, int n) {
// finish when all courses are taken
if (mask == ((1 << n) - 1)) return 0;
// Memorization of taken courses
if (bitmask[mask] != -1) return bitmask[mask];
// Initialize all vertices with indegree 0
std::vector<int> indegree(n, 0);
// Update the indegree
for (int i = 0; i < n; ++i) {
// skip the courses have been taken
if (mask & (1 << i)) continue;
for (auto &elem : relations[i]) indegree[elem] ++;
}
// For a mask of all courses with 0-indegree
int temp = 0;
for (int i = 0; i < n; ++i) {
// iterate through all the courses with zero indegree and have't been taken
if (indegree[i] == 0 && !(mask & (1<<i))) temp = temp | (1<<i);
}
int courses = temp;
// count of courses with 0-indegree
int count = __builtin_popcount(courses);
int semester = INT_MAX;
if (count > k) {
// (Overlapping sub-problem) iterate through all submasks (sub-problem) of temp
while (courses) {
courses = (courses - 1) & temp;
count = __builtin_popcount(courses);
if (count != k) continue;
semester = std::min(semester, 1 + find_min_semester(relations, bitmask, mask|courses, k, n));
}
} else {
semester = std::min(semester, 1 + find_min_semester(relations, bitmask, mask|courses, k, n));
}
return bitmask[mask] = semester;
}
int Solutions::minNumberOfSemesters(int n, std::vector< std::vector<int> > & relations, int k) {
// No dependencies
if (relations.size() == 0) return n % k == 0 ? n / k: n/ k + 1;
std::vector< std::vector<int> > adjacent(n);
std::vector<int> bitmask;
for (auto &course : relations) {
adjacent[course[0] - 1].push_back(course[1] - 1); // graph
}
// initial bitmask that all of courses haven't been taken
bitmask.assign(1<<n, -1);
return find_min_semester(adjacent, bitmask, 0, k, n);
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the minimal number of semesters are as follows:
- Initialize all cities without visiting
- DFS-based linear-time traverse neighbor city
- Count how many set is considered a connected city
Exercise 4 - Regular Expression Matching
Given an input string s and a pattern p, implement regular expression matching with support for ‘.’ and ‘*’ where:
- ’.’ Matches any single character.
- ‘*’ Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
Example: Input: s = “aacd”, p = “abcd*”, Output: true
Solution
isMatch.cc
bool Solutions::isMatch( std::string s, std::string p) {
int m = s.length();
int n = p.length();
// build our dp array depends on the current character in the pattern string
std::vector< std::vector<bool> > dp (m + 1, std::vector<bool>(n + 1, false));
dp[0][0] = true;
for(int i = 0; i <= m; i++) { // S
for(int j = 1 ;j <= n; j++) { // p
if(p[j-1] == '*') {
dp[i][j] = ( dp[i][j-2] )|| // repeats for 0 time
( i-1 >= 0 && dp[i-1][j] && ( s[i-1] == p[j-2] || p[j-2] == '.' ) ); // repeats for at least 1 time
} else {
dp[i][j] = i-1 >= 0 && dp[i-1][j-1] && ( s[i-1] == p[j-1] || p[j-1] == '.' ); // the pattern is the same
}
}
}
return dp[m][n];
}The solution was inspired by LeetCode Discuss. The basic functions for caculating the maximum profit are the same.
- Define the state dp[i][j] (two pointers pointing to the current characters at the string and pattern respectively) to be true if string s[0..i) matches pattern p[0..j) and false otherwise.
- Depend on the current character in the pattern string to reduce to subproblems:
- check the pattern repeats for 0 time or the pattern repeats for at least 1 time if the current character is *
- check the pattern is the same if the current character is not *
- The solution to given optimization problem can be obtained by the combination of optimal solutions to its sub-problems
Exercise 5 - Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Example: Input: coins = [1,2,5], amount = 11, Output: 3
Solution
coinchange.py
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [math.inf]*(amount+1)
dp[0] = 0
for a in range(1, amount + 1):
for coin in coins:
if a - coin >= 0:
dp[a] = min(dp[a], 1 + dp[a - coin])
return dp[-1] if dp[-1] != float('inf') else -1The solution was inspired by LeetCode Discuss. The basic functions for caculating the fewest number of coins that you need to make up that amount.
- Define the state dp[a] the fewest number of coins that you need to make up that a.
- Depend on the current coin in the coins to reduce to subproblems:
- check the the fewest number of coins that you need to make up that a
- The solution is determined by the recursive algorithm solving the problem, and should solve the same sub-problems over and over to obtain the fewest number of coins that you need to make up that amount.
=========== To be continued…. ==========
